PRTF - Perry Rhodan Technik Forum
Mögliches Wirkungsprinzip der "Quellen der Kraft" der Baolin-Nda
(c) Michael Gebinoga 01. 05. 2000
Zuletzt bei den Auseinandersetzungen um Thoregon und insbesondere bei den Kämpfen gegen die kosmische Fabrik MATERIA kamen Terraner erneut mit Ultra-High-Tech Erzeugnissen kosmokratennaher Mächte in Kontakt. Diese hochentwickelten Gerätschaften wurden von den Baolin-Nda im Auftrag der Kosmokraten oder ihrer Stellvertreter angefertigt. Bereits in früheren Jahren kamen die Terraner mit High-Tech Erzeugnissen der Baolin-Nda in Berührung. Beispiele sind die KASERNE des Kosmokraten Taurec - winzige Robotkämpfer, die sich durch Energieaufnahme aus der Umgebung zu mannsgroßen und kampfstarken Robotern aufblähen konnten, weiterhin wurden die Virtuellen Schiffe von den Baolin-Nda konstruiert und auch der sechsfingrige Handschuh, der bei den Auseinandersetzungen mit Seth-Apophis eine Rolle spielte. Später sagten sich die Baolin-Nda auf Betreiben eines Helioten von den Kosmokraten los und arbeiteten seit dem für Thoregon. Im Rahmen dieser Arbeiten wurden von ihnen die "Quellen der Kraft" konstruiert. Diese "Quellen der Kraft" dienen als Energieversorgung für Großgeräte wie beispielsweise den Heliotischen Bollwerken, wie sie von den Nonggo im solaren System kurzzeitig installiert wurden. Beschrieben wurden sie als kompakte, ultrahell strahlende Energiebälle, die vermutlich in einer speziellen Kraftfeldaufhängung verankert sind und den Energiebedarf der Heliotischen Bollwerke decken. Ob es für die Heliotischen Bollwerk noch weitere Energieversorger (NUGAS Reaktoren, Hypertrop-Zapfanlagen) gibt, ist nicht bekannt, da die Bollwerke durch Shabazzas Nanokolonnen (welche übrigens ebenfalls ein Produkt der Baolin-Nda waren) sabotiert und vernichtet wurden. Bei der Zerstörung der Bollwerke zeigte sich auch, dass die "Quellen der Kraft" eine Sicherung gegen ein "Durchgehen" dieser Superreaktoren beinhalten.
Die Frage nach der prinzipiellen Funktionsweise der "Quellen der Kraft" ist zur Zeit noch nicht beantwortet und man ist auf entsprechende Mutmaßungen angewiesen. Einige Vermutungen weisen in die Richtung, welche im Bericht über den "Hawking Projektor" angerissen wurden.
Bei den Berechnungen über den besagten "Hawking Projektor" zeigte es sich, dass Black Holes mit Massen zwischen einigen Millionen und einigen Milliarden Tonnen durchaus die Eigenschaften aufweisen können, welche bei den Quellen der Kraft beobachtet wurden. Klassisch gesehen sind Black Holes vollständig schwarz, d. h., Black Holes gelten als Orte von denen keine Strahlung mehr ausgehen kann, da selbst lichtschnelle Photonen aufgrund der Gravitation bzw. der geschlossenen Raumkrümmung nicht mehr entweichen können, wenn sie von außerhalb den Ereignishorizont des Black Holes durchstoßen haben. Bei quantenmechanischer Betrachtung sieht das ein wenig anders aus. Der Astrophysiker Stephen Hawking zeigte im späten 20. Jahrhundert AZ, dass aufgrund von Quanteneffekten Black Holes nicht vollständig schwarz sind, sondern eine massenabhängige Strahlung aufweisen. Bei dieser Strahlung handelt es sich jedoch nicht um die Strahlung, die von der ein Black Hole häufig umgebende Akkretionsscheibe aus Gas und Plasma ausgeht, sondern die direkt mit dem Black Hole im Zusammenhang steht.
Berechnungen zufolge strahlen Black Holes umso stärker, je
kleiner sie sind. Große Black Holes haben folglich eine
extrem geringe Strahlung und damit verbunden eine sehr hohe
Lebensdauer. Mikroskopisch kleine Black Holes hingegen - mit Massen
zwischen einigen Millionen und einigen tausend Tonnen und einem
damit zusammenhängenden Schwarzschildradius von einem
Attometer (1x10-18 m) und kleiner - verdampfen
fast schlagartig und die Restmasse wird vollständig in
Strahlungsenergie (hauptsächlich Gammastrahlung) umgesetzt.
Zur Erinnerung sei kurz erwähnt, dass ein Proton einen
Durchmesser von etwa einem Femtometer (1x10-15 m) hat.
Wir befinden uns also im Grenzgebiet zwischen den Abmessungen von
Elementarteilchen und der Planckschen Länge. In
Tabelle 1 findet man die Formeln, mit
denen man die Strahlungszeiten und Temperaturen bei Black Holes
abhängig von der Masse berechnen kann.
| m: Masse in kg; MSol : Sonnenmasse = 2 x 1030 kg |
(Formel 1) (Formel 2) (Formel 3) |
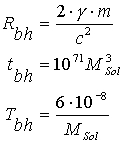 |
| Gravitationskonstante: g = 6.67 x 10-11(m3/kg s2) | ||
| Vakuum-Lichtgeschwindigkeit: c = 3 x 108 (m/s) | ||
| Plancksches Wirkungsquantum: |
||
| Plancksche Masse: mPl = 1019 GeV/c2 = 2.1 x 10 -8 (kg) | ||
| Plancksche Länge:lPl =
(g |
||
| Plancksche Zeit:tPl =lPl / c = 5.4 x 10 -44(s) | ||
| Rbh: Radius (Ereignishorizont) eines Black Holes in Meter (m) | ||
| tbh: Lebensdauer eines Black Holes in Sekunden (s) | ||
| Tbh: Strahlungstemperatur (Hawking Strahlung) eines Black Holes in Kelvin (K) |
Es ist ersichtlich, dass Schwarze Löcher mit Mindestmassen von Sonnen sehr kalt und sehr langlebig sind. Die folgenden Beispiele in Tabelle 2 zeigen aufgrund der Formeln 1 bis 3 die Eigenschaften (Radius, Lebensdauer, Strahlungstemperatur) von Black Holes unterschiedlicher Massen. Für die Massen wurde in entsprechenden Bruchteilen einer Sonnenmasse gerechnet. Die Berechnungen ergaben, dass selbst relativ kleine Black Holes von der Masse des Erdmondes noch eine Lebensdauer haben, die überastronomisch groß ist und eine Strahlungstemperatur, die noch unterhalb der 3 K Mikrowellen-Hintergrundstrahlung (Big Bang Echo) liegt. Wenn die Black Holes jedoch Massen im Bereich einer Planck Masse (unterhalb von 20 Mikrogramm Masse) aufweisen, kommt man folgerichtig in Bereiche der Planckschen Länge und der Planckschen Zeit. Die dazugehörigen Strahlungstemperaturen entsprächen gleichfalls denen beim Big Bang. Bei Zeiträumen, die kleiner als die Plancksche Zeit sind, findet man eine Aufhebung der Kausalität. Aufgrund des ineinander Übergehens von Raum und Zeit in diesen Dimensionen läßt sich nicht mehr feststellen, welches von zwei Ereignissen zuerst stattfand. Für unsere Zwecke ist jedoch der Massenbereich zwischen diesen beiden Extremen von Interesse. Kommen wir nochmal zurück zu Black Holes von stellarer Größe.
| Masse | Schwarzschildradius (Rbh) | Lebensdauer (tbh) | Strahlungstemperatur (Tbh)> |
| 1031 kg (5 Sonnenmassen) | 14.8 km | ca. 4 x 1064 Jahre | 1.2 x 10-8 K |
| 7*1022 kg (Masse von Luna) | 0.1 mm | ca. 4 x 1048 Jahre | 1.7 K |
| 200000 t (NUGAS Kugel) | 3 x 10-19 m | 27.7 h | 6 x 1014 K |
| 10.8 µg | 1.62 x 10-35 m (Planck-Länge) | 1.57 x 10-44 s | 1031 K |
Wird keine weitere Masse zugeführt, so würde ein
normales Black Hole mit der Zeit abdampfen. Die dafür
nötigen Zeiträume übersteigen aber die Lebensdauer
von Sternen um viele Größenordnungen.
Bei normalgroßen Black Holes würde dieser Effekt erst
dann zum Tragen kommen, wenn wir in einem offenen Universum leben
und dieses sich bis in alle Ewigkeit weiter ausdehnen würde.
Erst wenn die Restmasse nur noch sehr klein ist, kommt es zu
dramatischen Effekten.
Das Black Hole verliert immer mehr und immer schneller Masse, die
als Gammastrahlung infolge von Elektron-Positron
Annihilationsprozessen abgestrahlt wird.
Dabei wächst auch die Strahlungstemperatur sehr schnell an,
bis das Mikro Black Hole in einem gigantischen Hadronen-Feuerball
vergeht.
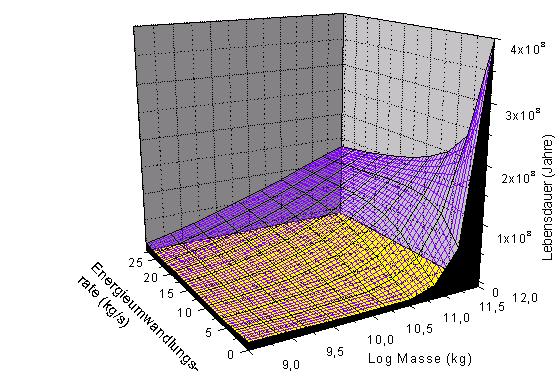
Abbildung 1: Gegenseitige Abhängigkeit des
Massenverlustes (entsprechend der Energieumwandlungsrate) eines
Black Holes durch Hawkingstrahlung mit der Masse und der
Lebensdauer des Black Holes (Masse-Skala in logarithmischer
Auftragung).
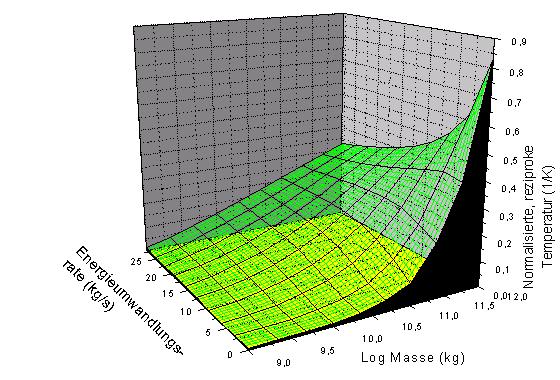
Abbildung 2: Verhältnis der reziproken Strahlungstemperatur eines Black Holes in Abhängigkeit von der Masse (Masse-Skala in logarithmischer Auftragung) und des Massenverlustes (entsprechend der Energieumwandlungsrate) eines Black Holes durch Hawkingstrahlung.
Aus den beiden Diagrammen ist abzusehen, dass für eine Energiegewinnung aus mikroskopischen Black Holes in Form von "Quellen der Kraft" einige Änderungen auf quantenphysikalischer Ebene vorgenommen werden müssen. Dies würde weiterhin bedeuten, dass "Quellen der Kraft" zum gegenwärtigen Zeitpunkt nicht von terranischen Wissenschaftlern konstruiert werden könnten. Eine Waffe wie der "Hawking Projektor" wäre aber machbar, da die nachfolgend aufgeführten Problempunkte für die Waffenentwicklung nicht relevant wären. Wir haben hier eine interessante Analogie zur Kernfusion. In der Mitte des 20. Jahrhunderts AZ war es zwar schon möglich thermonukleare Bomben herzustellen, jedoch fand die friedliche Nutzung der Kernfusion erst im ausgehenden 20. Jahrhundert AZ ihre Anfänge. Für die "Quellen der Kraft" und die mikroskopischen Black Holes gibt es die folgenden Problempunkte, welche sich auch aus den Abbildungen 1 und 2 ableiten lassen:
- Black Holes mit Massen oberhalb von 10 Millionen Tonnen haben nur einen relativ geringen Massenverlust von unter 0.25 kg/s und bieten folglich eine zu geringe Energiegewinnung für energieintensive Prozesse.
- Black Holes mit relativ hohen Energieproduktionswerten (> 3 kg/s = 2.7 x 1017 Ws) haben nur eine relativ kurze Lebensdauer von weniger als 10 Jahren.
- Black Holes strahlen mit der Zeit wachsende Energiemengen ab.
Das sich hieraus ergebende Problem sollte für die Baolin-Nda handhabbar sein, und darüberhinaus die Lösung für einige der angesprochenen Charakteristika beinhalten. Der entscheidende Punkt bei der Betrachtung ist die Wahrscheinlichkeit, mit der die die Hawkingstrahlung bedingenden Quantenfluktuationen nahe am Ereignishorizont eines Black Holes auftreten. Es handelt sich hierbei um Virtuelle Teilchen, dass heißt um Elementarteilchen, die aufgrund der Heisenbergschen Unschärferelation spontan und für sehr kurze Zeiträume im Vakuum entstehen. Diese Teilchen entstehen immer paarweise (Teilchen und Antiteilchen) und für ihre Entstehung "leihen" sie sich Energie aus den benachbarten Raumgebieten. Die Unschärferelation verlangt, dass sie ihre Energie schnell wieder zurückgeben, so dass sie normalerweise nicht eingefangen werden können. Die "geliehene" Energie wird zurückbezahlt, indem die Teilchen sich gegenseitig vernichten (Annihilation). Passiert diese Quantenfluktuation jedoch in der Nähe eines Black Holes, so kann es sein, dass die beiden virtuellen Teilchen innerhalb und außerhalb des Ereignishorizontes des Black Holes entstehen. In diesem Fall ist es möglich, dass das Teilchen außerhalb des Ereignishorizontes entfliehen kann und seine "Energieschulden" nicht bezahlt. Bezahlt wird in dem Fall vom Black Hole, welches einen kleinen Teil seiner Masse-Energie dabei verliert. Es ist unmittelbar einleuchtend, dass diese Effekte umso stärker wirken, je kleiner das Black Hole ist. Normalerweise sind diese Quanteneffekte nur von der Größe des Black Holes abhängig. Für sehr kleine Black Holes mit Massen unter einer Million Tonnen, deren Schwarzschildradius deutlich kleiner als der Durchmesser eines Protons ist, wachsen diese Quantenfluktuationen sehr stark an. Hätte man dagegen eine weitere - massenunabhängige - Möglichkeit, diese Quantenprozesse zu beeinflussen, entspräche das den Moderatorstäben bei einem normalen Kernspaltungsreaktor. Es wäre plausibel, wenn die Baolin-Nda die Möglichkeit hätten, diese Quantenprozesse im weiten Umfang zu steuern. In diesem Fall würde sich der Koeffizient aus der zweite Gleichung (s.o., Lebensdauer von Black Holes) verkleinern und auch größere Black Holes würden deutlich stärker (oder schwächer) strahlen. Weiterhin würde die Beeinflußung der Quantenprozesse auch den Sicherheitsmechanismus erklären. Ein Herunterfahren der Wahrscheinlichkeit von Quantenfluktuationen in der Nähe des Black Holes würde dieses Black Hole schlagartig abkühlen und den Energiestrom nahezu versiegen lassen. Weiterhin kann über eine Regulierung der Quantenfluktuation eine konstante Energieabstrahlung erreicht werden. Es ist nicht uninteressant, dass eine derartige Beeinflußung von Quantenfluktuationen sowohl bei der Entstehung der Thoregon-Vakuumblasen eine Rolle spielt, als auch bei der Gewinnung von ultimater Materie durch die kosmischen Fabriken.
Unter den geschilderten Voraussetzungen ließen sich Black Holes denken, welche Massen von einigen Dutzend Milliarden Tonnen hätten und die eine entsprechend lange Lebensdauer (einige hundert Jahre) gepaart mit hoher Energieproduktion (ca. 1020 J/s) aufweisen würden. Diese Energieproduktionsrate entspräche einem nicht unbeträchtlichen Anteil der gesamten Energieproduktion eines Hauptreihensterns (z.B. Sol mit ca. 3.6 x 1026 J/s). Die Größe dieser Black Holes wäre natürlich immer noch verschwindend klein und ihr Schwarzschildradius wäre nur wenig größer als der Radius eines Protons. Rein optisch würden sie aufgrund ihrer extrem hohen Strahlungsleistung jedoch deutlich größer erscheinen. Etwas flapsig könnte man von einer konstant explodierenden Supernovae im Westentaschenformat sprechen. Prinzipiell könnte man eine derartige "Quelle der Kraft" ohne Probleme auch über längere Zeiträume laufen lassen. Es müßte in dem Fall nur sichergestellt werden, dass in gewissen Zeitabständen dem Black Hole neue Materie zugeführt wird, oder dass man die Quanteneffekte in einem solchen Umfang zu steuern weiß, dass man damit auch Black Holes mit Massen deutlich über hundert Milliarden Tonnen als Energiequelle nutzen kann.
Literatur-
Perry Rhodan Romane 1876 - 1999
-
John Baez and Ilja Schmelzer, "Hawking Radiation" in Particle Physics in the UK(http://hepweb.rl.ac.uk/ppUK/contents.htm), (1994, 1997)
-
Claus Kiefer "Towards a Full Quantum Theory of Black Holes" in Black Holes: Theory and Observation, edited by F.W. Hehl, C. Kiefer, and R. Metzler (Springer, Berlin, 1998).
-
Stephen W. Hawking, "Particle creation by black holes", Commun. Math. Phys. 43 (1975), 199-220.

