PRTF - Perry Rhodan Technik Forum
Teil 5 der Manual of Science
HYPERSCHWINGUNGEN (1) - EINFÜHRUNG
(c) Rainer Castor 16.03.1998
Eine Schwingung wurde allgemein als Vorgang umschrieben, bei dem zwei Energiearten (beim Pendel z.B. kinetische und potentielle Energie) periodisch ineinander umgewandelt wurden, wobei die Ursache der Schwingung Kräfte waren, die physikalische Art der Schwingungsgröße für den Begriff der Schwingung aber gleichgültig blieb (Abb. 1).
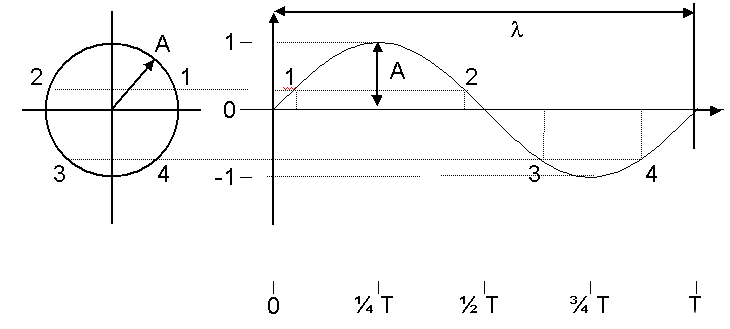 Abbildung 1:
Abbildung 1:
Harmonische Schwingung als Projektion einer gleichförmigen
Kreisbewegung am Einheitskreis
(U = 2p r , bei r = 1)
Verlief die Schwingungsgröße
sinusförmig mit der Zeit, sprach man von einer
Sinusschwingung.
Bei sinusverwandten Schwingungen änderten sich die
Amplitude und/oder der Phasenwinkel mit der Zeit; Beispiele waren
die gedämpfte Schwingung, die Schwebung und modulierte
Schwingungen (Funk etc.).
Für Sinuswellen galten z.B. neben der Frequenz die
Grundgrößen:
Kreisfrequenz - w= 2p * n [s-1 =
Hz] (Winkelgeschwindigkeit bei der Kreisbewegung, deren Projektion
die harmonische Schwingung war); die Einheit Hertz war der
reziproke Wert der Periodendauer T bzw. der
Quotient aus der Anzahl n der vollen Schwingungen
(Perioden) und der Zeitt, in der sie erfolgten: n =
n/t = 1/T;
Kreiswellenzahl - k = 2p / l
[m-1];
Auslenkung von der Ausbreitungsrichtung mit der
Amplitude (A) als Scheitelwert durch die
Wellengleichung:
x (x,t) = A * sin 2p (t/T - x/l ) [m].
Außerdem war die Phasengeschwindigkeit einer Welle
das Produkt von Frequenz und Wellenlänge:
vPh = n * l(bei elektromagnetischen Wellen:
vPh = c), und unter Einbezug des
Planckschen Wirkungsquantums h (»
6,626*10-34 Js) war eine Aussage zur
Quantenenergie (E) und ihren Impuls (p)
möglich (E = h * nund p = h / l): Bei
zunehmender Frequenz traten die Welleneigenschaften zurück,
die Strahlung verhielt sich mehr wie ein Korpuskelstrahl -
gleichzeitig nahm die Energie eines Quants, die bei kleinen
Frequenzen meist nicht ausreichte, um beobachtbare Effekte
hervorzurufen, mit der Frequenz zu, so daß bei kurzwelliger
Strahlung schon ein einziges Quant wesentliche Umwandlungen an
atomaren System auslöste.
Beispiel: Bei einer Frequenz von 1014 Hz betrug die Quantenenergie 6,626 * 10-20 J, bei einer Frequenz von 1020 Hz dagegen 6,626 * 10-14 J.
Weiterhin galt: Nach dem Fourier-Theorem konnte jede Welle als Summe von Sinuswellen dargestellt werden; hierbei war die Summe des Fourierspektrums eindeutig, d.h. es gab nur eine Möglichkeit, eine Welle in die »Sinuswellensprache« zu übersetzen.
...Ein Objekt kann entweder räumlich scharf lokalisiert, d.h. ein Teilchen, oder räumlich verteilt, d.h. eine Welle, sein... Die echte Synthese beider Bilder erfordert... eine »neue Dimension«, eine Erweiterung des Begriffssystems der Naturbeschreibung..., die durch das Plancksche Wirkungsquantum gegeben wurde ...Das Wirkungsquantum verbindet die Teilchen- und Welleneigenschaften der Mikroobjekte miteinander und gestattet so die Formulierung ihres komplementären Wesens... (Darüber hinaus) ...zeigte 1927 Heisenberg mit der von ihm aufgestellten Unbestimmtheitsrelation..., daß man einem Teilchen nur innerhalb der durch die Ungleichung bestimmten Grenzen einen bestimmten Impuls p und einen bestimmten Ort x gleichzeitig zuordnen kann... - sowie, als Erweiterung, daß eine gleiche Unschärfe hinsichtlich der Faktoren Energie E und Zeit t bestand [Aus: KLEINE ENZYKLOPÄDIE ATOM- UND KERNPHYSIK].
1928 fand Dirac einen mathematischen Ausdruck, der das zu dieser Zeit noch unentdeckte Positron vorhersagte ...Diracs Formel war - im Gegensatz zu den quadratischen Formeln der Relativitätstheorie - linear. In einer linearen Gleichen gibt es Plus- und Minusvorzeichen. Auf diese Weise wird die Asymmetrie beibehalten, die eine quadratische Gleichung, die eine Summe von Quadraten ist, ausfaktoriert (da das Quadrat eines Werts mit einem Minusvorzeichen immer ein Pluswert ist). Die Asymmetrie in der Diracschen Gleichung enthüllte das verborgene Positron... (In der Formel galt:)(...a und b sind Operationen, h ist die Plancksche Konstante, und i ist imaginär): ab - ba = ih
(Hierbei repräsentierte der Buchstabe i) ...die Quadratwurzel aus -1 ... Er besagt, daß die Wirkung von h andersartig ist als die durch ab und ba ausgedrückte Positionsänderung. i ist imaginär, d.h. in einer anderen Dimension befindlich...
...Unsere reduzierte Formel ab - ba = ih besagt also,
daß sich der Prozeß auf die materielle Ebene begibt
(ab) und sich wieder von ihr löst (-ba). Dabei produziert er
eine »nichtmaterielle« Wirkungseinheit... Die
Wirkung... erfolgt in diskreten ganzen Einheiten, die sich nicht
unterteilen lassen... Das Produkt aus Energie und Zeit ist
konstant. Dies ist die Plancksche Konstante und die Einheit der
Wirkung... Wirkung = E * t (Energie * Zeit) = konstant (h)
[Arthur Young, DER KREATIVE KOSMOS]
Die konventionelle Physik hatte ihr Gebäude maßgeblich auf drei Meßgrößen aufgebaut - Masse (m), Weg (s) und Zeit (t) - sowie auf deren vielfältige Kombinationsmöglichkeiten; gemäß der Relativitätstheorie war hierbei die Lichtgeschwindigkeit c als Konstante eng mit der Zeit verknüpft. Die Zeit wurde eindimensional behandelt und als Skalar betrachtet, d.h. als eine Größe durch eine Zahl angegeben. Von dieser Voraussetzung hing sehr viel ab, denn in der Physik waren alle Bewegungsgleichungen Differentialgleichungen nach der Zeit. Mit anderen Worten: Man müßte die gesamte Physik umschreiben, würde sich z.B. die Zeit als Vektor herausstellen, also als eine Größe, die neben dem Betrag eine »räumliche« Orientierung (Richtung) hatte (gemeint war hier nicht die unserem Zeitempfinden und auch den thermodynamischen Grundsätzen folgende Kennzeichnung eines »Zeitpfeils«, der kausal Vergangenheit von Gegenwart und Zukunft trennte!) [nach ebd.].
In der Masse-Energie-ÄquivalenzE = mc2 wurde über die Lichtgeschwindigkeit jeder Masse eine ihr äquivalente Energie zugeordnet (»Materie« bestand in diesem Sinne also aus den Teilkomponenten Masse und Energie), und beim Planckschen Wirkungsquantum h als fundamentale Konstante handelte es sich um die Aussage, daß jedes Quant eine Energie proportional seiner Frequenz (E = h * n) enthielt, oder - da die Frequenz der Kehrwert von Zeit war:
h war gleich dem Produkt aus Energie und Zeit (h = E * t = Wirkung). Die Einheit war hierbei [Js = Nms = kgm2/s], d.h. es wurden alle drei maßgeblichen konventionellen Meßgrößen in Form von ms2/t zueinander in Bezug gesetzt [ebd.].
Die Bedeutung der Wirkung lag in der ...Entdeckung Plancks, daß Wirkung in Ganzen oder Quanten erfolgt... Die Ganzheit - zusammen mit der Tatsache, daß die Wirkung Masse, Länge und Zeit als »Teile« enthält - ermöglicht uns die Aussage, daß Masse, Länge und Zeit von der Wirkung, vom Ganzen, abgeleitet sind. Die Zweckbestimmtheit, die zwangsläufig nicht im Teil existieren kann, läßt sich für das Ganze annehmen. Sie ist in der Tat gleichbedeutend mit der Funktion, die dem Ganzen - und nur dem Ganzen - zukommen kann... Die Ganzheit gehört zur Natur jeder Handlung, jeder Entscheidung, jeder zielgerichteten Aktivität. Plancks Entdeckung über das Licht gilt für unsere eigenen Handlungen und ihre Wirkung... Das Ganze kann nicht funktionieren, wenn es geteilt wird... So gelangen wir zu einem kosmologischen Grundpostulat: die Teile sind vom Ganzen abgeleitet, und nicht umgekehrt. Mit anderen Worten: das Ganze existiert vor den Teilen... Eine weitere Überlegung, die die grundlegende Natur der Wirkung bestätigt, ist die Tatsache, daß Wirkungen eigenschaftslos sind. Die Masse wird in Gramm, die Länge in Meter und die Zeit in Sekunden gemessen, Wirkungsquanten hingegen werden gezählt, wobei keine Notwendigkeit besteht, die Art der Einheit näher zu definieren. Darin wird ihre grundlegende Natur offenbar: die Wirkung geht dem Messen voraus, sie kommt noch vor der Analyse, die zu Angaben in Gramm, Metern und Sekunden führt... [ebd.]
Wissenschaft aber stand und fiel mit der Aufstellung von formalen Ausdrücken, die sonst nicht faßbare Zusammenhänge beschrieben. Newton lieferte den notwendigen formalen Ausdruck durch die Differentialrechnung, wobei er die Geschwindigkeit als das Verhältnis vom Weg zur Zeit und die Beschleunigung als das Verhältnis von Geschwindigkeitsveränderung zur Zeit definierte. Geschwindigkeit v war die erste Ableitung (des Ortes) s/t [m/s], Beschleunigung a die zweite Ableitung s/t2 [m/s2]. Zwar erwähnte er noch eine dritte Ableitung, ohne jedoch den Versuch zu machen, ihr physikalische Bedeutung zu verleihen. Weil jede Ableitung dem Verhältnis der abgeleiteten Größe zur Zeit entsprach, lag es nahe, in der dritten Ableitung das Verhältnis von Beschleunigung zur Zeit zu sehen, also s/t3 [m/s3]. Interpretation: Beschleunigung war die Änderung der Geschwindigkeit, eine Veränderung der Beschleunigung im weitesten Sinne »Kontrolle« - als solche nicht »vorhersagbar«, sondern von dem abhängig, der sie ausübte. Zwar unbestimmt, war sie dennoch eine zu beachtende Größe, denn »Kontrolle« war für den BEOBACHTER evident, der somit durch die dritte Ableitung ins physikalische System eingeführt wurde (Abb. 2) [ebd.].
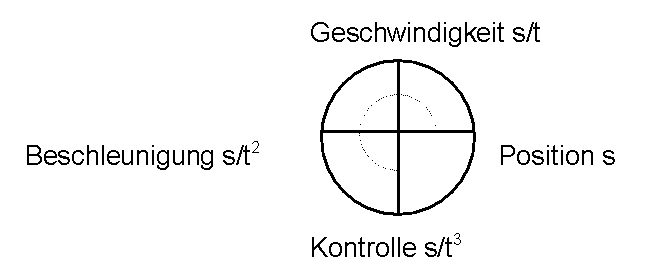 Abbildung 2
Abbildung 2
Während also »Kontrolle« nach ¾ eines Vollkreises (durchaus im Sinne eines »Einheitskreises« zu sehen) erreicht war, ließ sich aus der graphischen Darstellung erkennen, daß die vierte Ableitung mit dem Ort identisch war - was die Praxis bestätigte: Die »Kontrolle« der Beschleunigung wurde von einem Ort (dem angestrebten Ziel z.B. bei der Fahrt mit einem Gleiter) bestimmt. Bei s/t4 handelte es sich um einen »Identitätsoperator«, denn für die vierte Ableitung galt 360° = 0° = 2p, und dies ließ sich auch als Zyklus oder Wirkungszyklus auffassen, wie die Darstellung einer Schwingung am Einheitskreis zeigte.
In der Quantenmechanik wurde das Wirkungsquantum häufig als auf den Umfang des Einheitskreises bezogene kleinste Wirkung dargestellt, so daß für »h-quer« galt:
![]() (= 1,05459*10-34 [Js])
(= 1,05459*10-34 [Js])
Diese 2p hatten jedoch noch eine weitere Bedeutung, auf die
schon der Astronom, Mathematiker und Physiker Sir Arthur Stanley
Eddington (1882-1944) in seiner 1946 posthum erschienenen
Fundamental Theory hinwies: In Überwindung des
Konflikts zwischen der Betonung des Kontinuierlichen bei der
Relativitätstheorie und der des Diskreten in der
Quantentheorie, führte er nach Arthur Young aus,
...daß das neue Konzept, das der Krümmung Rechnung
trägt, die Phase ist, und Phase-Raum stellt eine
fünfte Dimension dar, die zur Raum-Zeit-Dimension im rechten
Winkel steht. Die Phase ist natürlich eine Winkelbeziehung und
kann zwischen 0 und 360° oder 2p variieren... [ebd.] Eddingon
wörtlich: Eine Winkelkoordinate hat das Merkmal, daß
die »unendliche Unsicherheit« einer uniformen
Wahrscheinlichkeitsverteilung zwischen 0 und 2p
entspricht...
[Fundamental Theory]
...Die Phase kann die Richtung sein oder... der zeitliche Abstand zwischen einem Input und einer Reaktion. Da sich die Wahl entweder in Richtung oder in Timing ausdrückt, läßt sie sich mit der Phasendimension gleichsetzen... Wir können mit unserer Argumentation noch einen Schritt weiter gehen: unsere Unsicherheit darüber, wie sich jemand anders entscheiden würde, läßt sich auch in Form eines Winkels ausdrücken, und die maximale Unsicherheit wäre gleich dem Winkel 2p ... Diese Unsicherheit gilt für jede Messung. Wohlgemerkt: es handelt sich um die Unsicherheit des Beobachters, auf das Objekt selbst bezogen ist sie Freiheit... Wie Eddington hervorhob, läßt sich die Krümmung der Raum-Zeit durch die Phasendimension ersetzen, deren Maß 2p ist, und dieser Wert von 2p entspricht der zur Quantentheorie gehörenden Unsicherheit. Mit anderen Worten: Eddington erkannte, daß die Krümmung in der Relativitätstheorie dasselbe ist wie die Unsicherheit in der Quantentheorie! Wie steht es aber nun mit der Skala? Sicherlich ist die mikroskopisch kleine Unsicherheit eines einzelnen Protons nicht dasselbe wie die riesige Krümmung des Raum-Zeit-Gebildes, das erst nach Milliarden von Jahren sich »wiederholt« bzw. seinen Zyklus abschließt. Es stimmt aber, daß beide in topologischer Hinsicht gleich sind! Ob wir uns nun mit einem Teilchen oder dem aus Teilchen bestehenden Universum befassen, wir erhalten die Topologie des Torus!... [Arthur Young, DER KREATIVE KOSMOS]
Die Volumenformel eines Einsteinschen Universums (Hypersphäre, sphärischer Raum) lautete: 2p2r3. Dem entsprach aber die eines TORUS (Ring mit kreisförmigem Querschnitt), sofern es sich um einen solchen handelte, dessen Loch »unendlich klein« wurde:
VTorus = 2p2r2R (R =
Ringradius; sofern das Loch gegen 0 ging, wurde R = r, dem Radius
des
kreisformigen Querschnitts)
Ausgehend davon, daß sich alles Physische als Kugel
»ausdrückte« (sei es, ob es sich um die
»Form« eines Teilchens oder um den
»Wirkungsradius« eines Lebewesens handelte),
mußte der Übergang vom Volumen einer 3D-Kugel (=
4/3pr3) zu dem einer
Hypersphäre mittels der Faktoren ¾ und
2perfolgen - und diese waren aus anderem Zusammenhang
wohlvertraut:
¾ war »Kontrolle« bzw.
»Selbstbegrenzung« (s/t3), von Eddington
»Skalenstabilisierung« genannt, und wurde nach ¾
eines Wirkungszyklus erreicht, der Veränderung der
Beschleunigung (damit auch Kontrolle von Kraft, weil
für Beschleunigung Kraft erforderlich war - F = m*a =
m*s/t2 [kgm/s2] - a = F/m = m*s/t2
/ m = s/t2 [m/s2]), während
2p als Identitätsoperator (360° = 0° = Umfang des
Einheitskreises = »Wirkung«) auftrat, nach Eddington
die »Phasendimension senkrecht zur Raum-Zeit« (d.h.
4D-Raum-Zeit + Phasendimension = 5D), so daß
»Wirkung« = Energie * Zeit = ms/t2 * st =
ms2/t = h war.
Der Meßformel ms2/t wiederum entsprach der Drehimpuls, also der Impuls eines in Kreisbewegung befindlichen Körpers. Im Gegensatz zum linearen Impuls (dem Produkt von Masse und Geschwindigkeit) war beim Drehimpuls der Impuls so »verpackt«, daß er keine Übertragungsgeschwindigkeit für seine Existenz benötigte.
Beispielsweise besaß ein Schwungrad einen Drehimpuls und
speicherte Energie, obwohl es am selben Ort blieb; andererseits
konnte das Schwungrad transportiert werden und somit die
gespeicherte Energie von
A nach B übertragen. Und damit ...erhalten wir eine
Antwort auf die seit langem gestellte Frage, wie sich die Wirkung
über Entfernungen überträgt. Nach dieser Theorie
nämlich enthält das Licht Energie in seinem Drehimpuls
und kann somit diese Energie von einem Punkt zum anderen
transportieren. Newtons Korpuskulartheorie vermochte die
Übertragung unterschiedlicher Energiemengen nicht zu
erklären, da sich die Korpuskeln alle mit der gleichen
Geschwindigkeit - der Lichtgeschwindigkeit - fortbewegen
müssen... Die Wellentheorie hingegen konnte die
Energieübertragung nur erklären, indem sie einen
unendlich festen Äther postulierte...
[Arthur Young, DER KREATIVE KOSMOS]
Die Größe der gespeicherten Energie war hierbei abhängig vom Radius der Drehbewegung - genau wie ein Schlittschuhläufer durch Anziehen der Arme die Drehung beschleunigte und damit seine Energie erhöhte; nach oben war die Grenze insofern festgesetzt, weil die Arme nur bis zu einem bestimmten Punkt angezogen werden konnten. In ähnlicher Weise konnte ein Teilchen, das keine Ruhmasse besaß - z.B. ein Lichtquant -, beliebig »zusammenschrumpfen«, d.h. je »kleiner« es wurde, desto mehr Energie beinhaltete es [nach ebd.].
Weil Schwingungen allgemein als periodischer Wechsel von einer Energieart in die andere dargestellt wurden und sich als Wellen - sofern das Medium keine Randbedingungen erzwang - mit charakteristischer Geschwindigkeit im Raum ausbreiten konnten, war eine Welle auch unmittelbar als Energietransport zu deuten; die Wellenenergie verhielt sich hierbei wie das Quadrat der Amplituden (Verdopplung der Amplitude einer Welle = Vervierfachung der Energie).
Bei dieser allgemeinen Betrachtung beachteten wir (zunächst) nicht, daß in der Quantenmechanik die Wellenfunktion y (psi) eines Quantenobjekts (= Lösungsfunktion einer Schrödinger-Gleichung) keine Energie transportierte und deshalb direkt nicht nachweisbar war (»beobach-tet« wurden Quantenteilchen, nicht Quantenwellen!); das Absolutquadrat der Amplitude einer Quantenwelle |y |2 war ein Maß für die Wahrscheinlichkeit (die Wellenfunktion wurde deshalb oft auch Wahrscheinlichkeitswelle genannt). Aus dem kontinuierlichen Verlauf einer Welle ergab sich, daß sie keine Teile hatte und deshalb beliebig zerlegt werden konnte, d.h. daß die Art von Teilen, die eine Welle zu haben schien, davon abhing, wie sie in Quanten zerlegt wurde.
Masse-Energie-Äquivalenz, Welle-Teilchen-Dualität,
Unbestimmtheitsbeziehung, Quantelung und allgemeine Feldtheorien
beschrieben eine Welt, deren essentielle Wirklichkeit eine Menge
von Feldern war, die, wenn man sie »quantelte«, ein mit
ihnen zusammenhängendes Quantenteilchen beschrieben. Die
Stärke eines Feldes an einem bestimmten Punkt im Raum war
gleich der Wahrscheinlichkeit, an dieser Stelle das mit ihm
zusammenhängende Quantenteilchen zu finden, so daß
Felder die Wahrscheinlichkeitswellen für ihre Quantenteilchen
waren. Die Wellenfunktion war nichts Materielles, sondern
gab nur die Wahrscheinlichkeiten materieller Ereignisse
an
[nach Heinz P. Pagels, DIE ZEIT VOR DER ZEIT].
Abschließend ein erstes Resmuee: Bevor von den allgemeingültigen Aussagen zu Schwingungen und den ihnen zugrundeliegenden Aspekten zu den Hyperschwingungen übergegangen wird, soll an dieser Stelle festgehalten werden, daß sich die mit der Hyperphysik verbundenen Grundaussagen problemlos aus dem Bekannten ableiten ließen.
So wie die Eddingtonsche »Vereinigung« von Relativitätstheorie und Quantenmechanik unter Berücksichtigung der maßgeblichen Faktoren ¾ und 2pund der Diracsche Formalismus, der den imaginären Aspekt von Wirkung beschrieb (ab - ba = ih), zu einem fünfdimensionalen Kontinuum führten (dessen Homogenität im Sinne einer höheren Symmetrie des Ganzen, das »vor« den Teilen existierte, betrachtet werden mußte), gelangten die Arkoniden durch Beobachtung und Auswertung hyperphysikalischer Phänomene ebenfalls zum 5D-Hyperraum, seiner Singularität und der Hyperenergie (= »Energie mit hyperphysikalischem Vorzeichen« bzw. »imaginäre Energie«), die als Ausdruck von Nicht-Lokalität aufgefaßt wurde. Sie war Ausdruck einer inneren Verbundenheit von allem mit allem, so daß sie unvermittelt, ungeschwächt und unmittelbar wirkte und erst bei Interaktion mit konventionellen Objekten als Wirkung ins Standarduniversum eintrat, verbunden mit zwangsläufiger »Degeneration« bzw. »Erstarrung« (Ekonv. wuchs, Ej nahm ab; im Extrem zu lim. Ej - 0), so daß es beim Übergang in raumzeitliche Dimension zu immer größerer Heterogenität kam (der »spontanen Symmetriebrechung« mit Auszeichnungen von »Richtungen in Raum und Zeit«), also der Ausrichtung auf die Teile, die meßbar waren.
Zwar galt für den Hyperraum an sich
die »Randbedingung« von t = 0 und E = ¥
gemäß den mit
Dimensionen n > 3 verknüpften dimensionsgeometrischen
Aussagen, doch eine »periodische Aktivität«
zwischen Ekonv. und Ej entsprach hierbei
einem der konventionellen Schwingung vergleichbaren Phänomen,
dessen Wirkungszyklus von 2pgenau wie eine
harmonische Schwingung als Projektion einer gleichförmigen
Kreisbewegung angesehen werden konnte. Daß zur weiteren
Erfassung und Darstellung wiederum
»Hilfskonstruktionen« notwendig waren, wie
grundsätzlich im Zusammenhang mit der Hyperphysik, ist Thema
des nächsten Teils dieses Manuals.
Vorwort 1 - 2 - 3 - 4 - 6 - 7 - 8 - 9 - 10 - 11 - 12

